Der Strömungsbereich ist in Fig. 2 gezeigt. 1. Zuerst wird die quadratische rechteckige zylindrische Geometrie mathematisch konstruiert, deren Länge 1 m, Breite 4 m beträgt, dann wird ein Quadrat mit einer Länge von 0,15 m an der Position (0,25 m, 0,2 m) gezeichnet. Die Differenz zwischen diesen beiden Zahlen wird gemacht und dann wird die gesamte Region markiert. Im nächsten Schritt werden im Abschnitt Materialeigenschaften die Eigenschaften der Flüssigkeit hinzugefügt. In Abbildung 1 haben die Grenzschichten eine Geschwindigkeit u Null. Die Randbedingung wird als kein Schlupf betrachtet und der Anfangsdruck ist Null. Im Einlauf wird eine Durchflussgeschwindigkeit von 1 m/s vorgegeben und die Auslaufbedingung gewählt. Um die Naiver-Stokes-Gleichungen zu lösen, wird die Strömungsphysik hinzugefügt. Abbildung 1 zeigt die Grenzen des Strömungsbereichs.
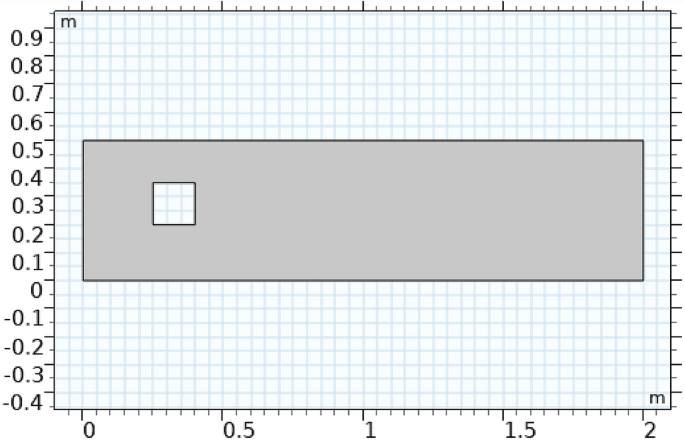
Der Umriss des Problems.
Die Position des rechteckigen und quadratischen Zylinders ist wie folgt:
Rechteck: Position (0,0) Breite (4 m); Höhe (1 m) und Größe (4,1).
Quadrat: Position (0.25,0.2) Seiten (0.15).
Die Randbedingungen am äußeren Rand sind wie folgt:
Region ‚Domänenstart ‚außerhalb‘ (0,0).
{Spiegelzustand an unterer Grenze}.
natürlich (\(u_{r} )\) = 0, natürlich (\(u_{\theta} ) =\)0, Wert Siez= 0.
Natürlich (p) = 0, Linie nahe Punkt (2.0).
Kein Seitenschlupf (dh Geschwindigkeit = 0) Wert Sier= 0bei dem die \(u_{\theta} = 0\)Siez= 0.
Natürlich (p) = 0 Linie nahe Punkt (2,0,5) Natürlich (Sier)=0natürlich (\(u_{\theta}\)= 0),
Wert (ur) = 0, natürlich(p) = 0. die zu schließende Linie (0,0,5).
Bienet=0; Sier=0, \(u_{\theta} = 0\)Siez=0, S=0.
Biener=0,2, z=0,25, u=-SIEÖn.
Die Widerstands- und Auftriebsbeiwerte sind definiert als:
$$C_{D} = \frac{{2F_{D} }}{{\rho U_{mean}^{2} D}},\quad C_{L} = \frac{{2F_{L} }} {{\rho U_{Mittelwert}^{2} D}}.$$
Die Kontinuitätsgleichung lautet:
$$\frac{\partial p}{{\partial t}} + \nabla .\left( {\rho u} \right) = 0,$$
(1)
Die Wärme- und Impulsgleichung lautet:
$$\rho C_{p} \left( {\frac{\partial T}{{\partial t}} + u.\nabla T} \right) + \nabla .\left( {q + q_{r} } \right) = \alpha_{P} T\left( {\frac{\partial P}{{\partial t}} + u.\nabla P} \right) + \tau .\nabla u + Q$$
(2)
$$\rho \frac{\partial u}{{\partial t}} + \rho \left( {u.\nabla } \right)u = \nabla .\left[ { – pi + k} \right] + V,$$
(3)
$${\text{true }}\;K = u\links[ {\nabla u + \left( {\nabla u} \right)^{T} } \right] – \frac{2}{3}u\left( {\nabla .u} \right)u.$$
(4)
Die Kontinuitäts- und Impulsgleichungen werden auf die folgenden Formen reduziert:
$$\frac{{\partial u_{r} }}{\partial r} + \frac{1}{r}u_{r} + \frac{{\partial u_{z} }}{\partial z} = 0,$$
(5)
$$\frac{{\partial u_{r } }}{\partial t} + u_{r} \frac{{\partial u_{r} }}{\partial r} + u_{z} \frac{{ \partial u_{r} }}{\partial z} – \frac{{u_{\theta }^{2} }}{r} = – \frac{1}{\rho }\frac{\partial P} {{\partial r}} + \frac{4}{3}\vartheta \frac{{\partial^{2} u_{r} }}{{\partial r^{2} }} + \vartheta \left ( {\frac{{\partial^{2} u_{\theta } }}{\partial r\partial z} + \frac{{\partial^{2} u_{r} }}{{\partial z^ {2} }}} \right),$$
(6)
$$\frac{{\partial u_{\theta } }}{\partial t} + u_{r} \frac{{\partial u_{\theta } }}{\partial r} + u_{z} \frac {{\partial u_{\theta } }}{\partial z} + u_{r} u_{\theta } = \vartheta \left[ {\frac{{\partial^{2} u_{\theta } }}{{\partial z^{2} }} + \frac{{u_{\theta } }}{{r^{2} }}} \right] + \vartheta \frac{{\partial^{2} u_{\theta } }}{{\partial z^{2} }},$$
(7)
$$\frac{{\partial u_{z} }}{\partial t} + u_{r} \frac{{\partial u_{z} }}{\partial r} + u_{z} \frac{{ \teilweise u_{z} }}{\teilweise z} = \vartheta \left[ {\frac{{\partial^{2} u_{r} }}{{\partial z^{2} }} + \frac{{\partial^{2} u_{z} }}{\partial r\partial z}} \right] + \frac{4}{3}\vartheta \frac{{\partial^{2} u_{z} }}{{\partial z^{2} }} – \frac{1}{P}\frac{ \partial P}{{\partial z}}.$$
(8)
Die für die Wärmegleichung verwendeten Transformationen sind:
$$\begin{aligned} & \alpha_{p} = – \frac{1}{\rho }\frac{\partial P}{{\partial T}},\;\sigma = – \rho I + \ tau,Q_{p} = \alpha_{p} T\left[ {\frac{\partial P}{{\partial t}} + u.\nabla P} \right],Q_{vd} = \tau .\Updelta u, \\ & q = – d_{m} k\Updelta T,\; d_{m} = 1m^{2} .P_{r} = \frac{K}{{\rho C_{p} }},\;\eta = \frac{{z(\Omega \sin \alpha^ {*} )^{0.5} }}{{V^{0.5} (1 – st\Omega \sin \alpha^{*} )^{0.5} }}, \\ & G = (\Omega \sin \ alpha^{*} )^{ – 1} (1 – st\Omega \sin \alpha^{*}, \\ & T\left( {t,r,z} \right) = T = \left( { T_{\omega } – T_{\infty } } \right)\theta,T_{\omega } – T_{\infty } = \left( {T_{0} – T_{\infty } } \right)\frac {x}{L}(1 – st^{*} )^{ – 2} \\ \end{aligned}$$
(9)
Nach der Transformation erhalten wir,
$$\begin{aligned} & Pr(\theta^{\prime \prime } ) = \nu \left( {\frac{1}{2}\theta^{\prime } \eta + 2\theta s} \right) \\ & \quad – pr\frac{G\nu }{{k_{f} \left( {T_{w} – T_{\infty } } \right)}}\left[ {\left\{ {\frac{{q_{0} }}{{A_{s} \Delta T}}} \right\} – p\left\{ {\frac{{u_{r} }}{r} + \frac{{\partial u_{r} }}{\partial r} + \frac{{\partial u_{\theta } }}{\partial z}} \right\} – \frac{1}{3}\left\{ {\frac{{\partial u_{z} }}{\partial z}\frac{{\partial^{2} u_{\theta } }}{{\partial^{2} z}} – 3\frac{{u_{\theta } }}{r}\frac{{\partial u_{r} }}{\partial z} – \frac{{\partial^{2} u_{r} }}{{\partial^{2} z}}} \right\}} \right] \\ & \quad + pr\frac{1}{{k_{f} \left( {T_{w} – T_{\infty } } \right)}}\frac{1}{{R_{e} } }\links[ {\frac{{\partial^{3} }}{{\partial r^{3} }}\left( {\frac{4}{3}u_{r} + u_{\theta } + u_{z} } \right) + \frac{1}{3}\left( {\frac{{u_{\theta } }}{r}\frac{{\partial^{2} u_{\theta } }}{{\partial^{2} r}} + \frac{{\partial u_{r} }}{\partial z}\frac{{\partial^{2} u_{\theta } }}{{\partial^{2} r}} – \frac{{u_{\theta } }}{r}\frac{{\partial u_{\theta } }}{\partial r}} \right) + \left( {\frac{{u_{\theta } }}{r}} \right)^{2} + \frac{4}{3}\left( {\frac{{u_{r} }}{r}} \right) + \frac{4}{3}\frac{{\partial u_{\theta } }}{\partial z}} \right] \\ \end{aligned}$$
(10)


